1800 419 9397
Job Oriented Training
Tutorial Of The Set Interface On Java
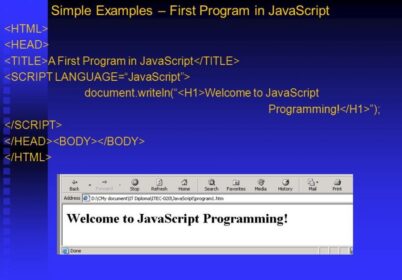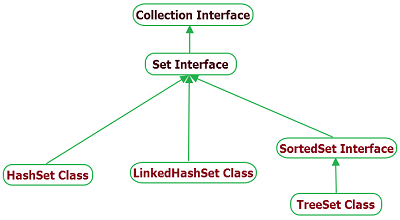
A set is a collection which cannot contain duplicate elements. It will model the mathematical set abstraction. Set Interface in java will have methods which are taken from Collection adding restriction which is prohibiting addition of duplicate elements.
Set will also add a stronger contract on the behavior of the equals as well as hashCode operations, allowing Set instances for comparing meaningfully even if their implementation types may differ.
The platform Java will contain three general-purpose Set implementations: HashSet, TreeSet and LinkedHashSet. HashSet which will store its elements right in the hash table and is one of the best-performing implementation; but there is no guarantee as far as the order of iteration is concerned. TreeSet stores the elements in red-black tree ordering the elements based on the values but it is slower than HashSet. In the similar way LinkedHashSet is implemented as a hash table right with linked list and will run through it and will order the elements based on the order which are inserted right into the set.
LinkedHashSet will spare its clients from the unspecified ordering as provided by HashSet at a price higher than usual.
The Set ADT
If the definition of the set interface model is justified then add() method will return false if there an attempt made for adding the duplicate elements right to the set. This will not define any additional method right of its own. Set is a interface which is generic which had this declaration:
Interface Set<E>
In this case, E will specify the type of objects which the set will hold. The Java Collections Framework will define the java.util.Set interface, which will surely include the fundamental methods:
- add(e): Adds the element e to S (if not already present).
- remove(e): Removes the element e from S (if it is present).
- contains(e): Returns whether e is an element of S.
- iterator( ): Returns an iterator of the elements of S.
There is again issue for support for traditional mathematical set operation of union, intersection, and subtraction of two sets T and S:
- S∪T = {e: e is in S or e is in T},
- S∩T = {e: e is in S and e is in T},
- S−T = {e: e is in S and e is not in T}.
In the java.util.Set interface, these operations are usually provided right through the following methods, if executed right on set S.
- addAll (T): Updates S for including all the elements of set T, effectively by replacing S by SuT.
- retainAll (T): Updates S so that it will only keep those elements which are also elements of set T by replacing S by S∩T.
- removeAll (T): Updates S by removing all of the elements which will occur in set T by replacing S by S-T.
The HashSet Class
Hashset will extend AbstractSet and will implement the Set interface. It will create a collection which will use the hash table for storage. HashSet is usually a generic class which has this declaration:
class HashSet<E>
E will specify the type of objects which the set will hold. As various readers know, has table will store information with the mechanism called hashing. In hashing, the Informational content of key is used for determining a unique value called the hash code. The hash code is used as index with which the data is associated for storing the key. The transformation of the key is stored into the hash code which is performed automatically- one will never see the hash code itself. The code cannot directly index the hash table. The advantage of hashing will allow it for execution time of add (), contains (), remove (), and size () to remain constant for large sets.
The Following Constructors Are Defined:
HashSet( )
HashSet(Collection<? extends E> c)
HashSet(int capacity)
HashSet(int capacity, float fillRatio)
The first form will constructs a default hash set. The second form will surely initialize the hash set with the use of the element of c. The third form will initializes the capacity of the hash set to capacity. There is the fourth form which will initialize both the capacity and the fill ratio of the hash set right from the arguments. There the fill ratio must be between 0.0 and 1.0 and will determine how full the hash set can be right before it is resized upward. When the number of elements is greater than the capacity of the hash set which is multiplied by the fill ratio then the hash set is expanded. HashSet will not define any additional methods beyond those which are provided by the superclasses and interfaces.
It is important to note that HashSet will not guarantee the order of the elements because the process of hashing does not lend itself right to the creation of sorted sets. If there is need for sorted storage then another collection such as TreeSet is a better choice. Here is example which will demonstrate HashSet:
// Demonstrate HashSet.
import java.util.*;
class HashSetDemo {
public static void main(String args[]) {
// Create a hash set.
HashSet hs = new HashSet();
// Add elements to the hash set.
hs.add("B");
hs.add("A");
hs.add("D");
hs.add("E");
hs.add("C");
hs.add("F");
System.out.println(hs);
}
}
The following is the output right from the program:
[D, A, F, C, B, E]
These elements are not stored in sorted order and so the precise output may vary.
The LinkedHashSet Class
The LinkedHashSet class will extends Hashset and it add no members of their own. It is generic class which has this declaration:
class LinkedHashSet<E>
Here, E will specify the type of objects which the set will hold. Its constructors will be parallel to those in the HashSet. LinkedHashSet will maintain a linked list of entries right in the set right in the order in which they were inserted. This will allow insertion-order interation over the set. When cycling through a LinkedHashSet with the use of iterator, the element will return in the order in which they were inserted. This is also the order which are contained in the string returned by toString() when called on LinkedHashSet object. For seeing the effect of LinkedHashSet, try using LinkedHashSet for HashSet in the program. The output will be [B, A, D, E, C, F] which will be in order for the elements which were inserted.
Also Read,
